Curvature of Spacetime

How We Understand Spacetime Today

To explain the curvature of spacetime, scientists use the analogy of a sphere distorting spacetime. The internet images below show that this representation is common.

These metaphors are interesting because they show that the deformation of spacetime is produced by volume, not by mass. Indeed, the mass is not represented in these graphs.

If we think in terms of masses, as academic physics considers, these figures do not explain the origin of the phenomenon of the curvature of spacetime by mass. Hence the question: how can a mass distort spacetime?

Spacetime Curvature: A Modern Mystery

Imagine a glass of water filled to the brim. The water represents spacetime. Now, drop a ball into the glass. What causes the water to overflow—the ball’s volume or its mass? Clearly, it’s the volume.

According to general relativity, spacetime distortion is caused by mass, not volume, which raises a paradox. Hence the question:

• Is spacetime curved by volume? This idea aligns with common sense, as illustrated by the ball-in-water analogy, but it contradicts Einstein’s general relativity.
• Is spacetime curved by mass? This view is fully consistent with general relativity, yet it defies intuition. Saying that the ball’s mass causes the water to overflow makes little sense. Regardless of the material — wood, iron, or otherwise — the overflow is due to the ball’s volume, not its mass.

Solution to this Enigma

The reality is that spacetime is distorted by the closed volumes discussed in the previous chapter. There is no contradiction, because:

• Closed Volumes, or "massive volumes": These are the volumes that curve the environment in which they are immersed. Note: not all volumes have this effect. Only closed volumes—and, in some cases, apparent and hermetic volumes—contain mass.
• Mass: Since mass is present within closed volumes, this concept aligns perfectly with General Relativity.

These are the closed volumes (or massive volumes) that curve spacetime.

This proposal reconciles mass, as described by Einstein’s General Relativity, with volume, as understood through common sense. If needed, refer back to the definitions of volume on the previous page

Note: Open volumes are transparent to spacetime because they are void. For this reason, they are ignored in this section.

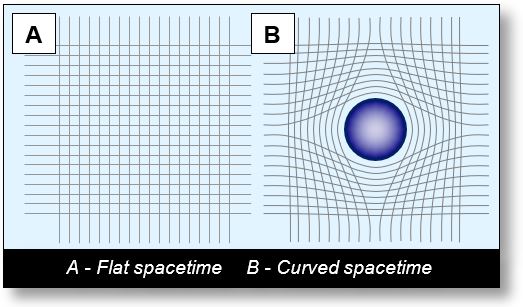
Minkowski vs. Einstein Spacetime

The differences are:

• Fig. A: Minkowski spacetime is empty and linear, as it contains no closed volumes.
• Fig. B: A corpuscle, such as an electron or nucleon, introduces closed volumes, thereby transforming Minkowski spacetime into Einsteinian (or Riemannian) spacetime. Since spacetime cannot penetrate these volumes, it curves around them—like water displaced by a ball in a full glass.

The Apparent Volumes Confusion

Apparent volumes differ from closed volumes by their mix of mass and vacuum. Their spacetime curvature depends on this ratio, which directly impacts calculations.

To understand curvature, ask: What causes it? Not mass, but closed volumes—like a ball displacing water in a full glass.

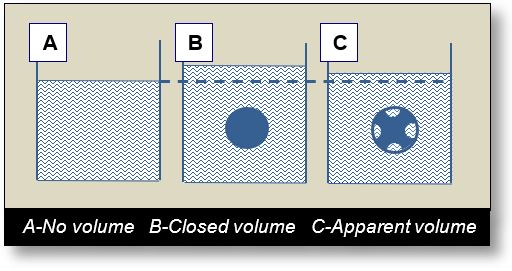
Ensure the appropriate volume type is used in calculations, i.e., open (Fig. A), closed (Fig. B), apparent (Fig. C), or hermetic (not shown) volumes.

Understanding Apparent Volumes in Spacetime

Spacetime curvature in apparent volumes depends on their closed volume content. The ball example illustrates this:

• Fig. A (above): Minkowski spacetime with only open volumes—no curvature.
• Fig. B: A closed-volume ball in water raises the level by its full volume.
• Fig. C: A perforated ball becomes an apparent volume. If 20% is open, water rises by 80% of its volume. Spacetime behaves similarly, curving in proportion to the closed part.

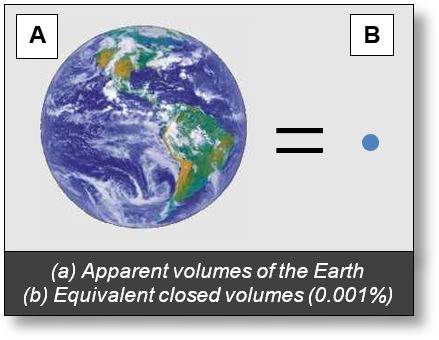
Earth as an Apparent Volume

Two representations of Earth illustrate how spacetime curvature relates to apparent volume:

• Fig. A: Earth is an apparent volume, composed of atoms that are 99.999% vacuum—represented by orbitals, which are open volumes—and 0.001% matter, consisting of a nucleus and electrons, which are closed volumes.
• Fig. B: Shows only the closed volumes—nucleus and electrons—representing 0.001% of Earth’s total volume. Only the closed volumes, i.e. "massive volumes", contributes to spacetime curvature. Open volumes are excluded, as they do not affect spacetime.